[Coding017] 递归 - Fibonacci数列
递归知识点

Ben 2024/01/01

More coding records
Get the knowledge flowing and circulating! :)

知识点※ 本题收获代码（4种实现方法）代码1（C语言经典递归 - 2种写法）代码2（C语言经典递归 - 计时版）代码3（C语言非递归 - 计时版）代码4（Java语言非递归 - 计时版）★ 知识点积累 (Java static方法的调用)

知识点

维基百科 - 斐波那契数
斐波那契数（意大利语：Successione di Fibonacci），又译为菲波拿契数、菲波那西数、斐氏数、黄金分割数。所形成的数列称为斐波那契数列，又译为菲波拿契数列、菲波那西数列、斐氏数列、黄金分割数列。这个数列是由意大利数学家斐波那契在他的《算盘书》中提出。
特别指出：0不是第一项，而是第零项。
斐波那契数列（Fibonacci）介绍：
$\begin{matrix} F (0) = 0 \\ F (1) = 1 \\ F (n) = F (n - 1) + F (n - 2) (n \geq 2 ， n \in N^{*}) \end{matrix}$
序号 0 1 2 3 4 5 … 40 50
数值 0 1 1 2 3 5 … 102334155 12586269025

序号	0	1	2	3	4	5	…	40	50
数值	0	1	1	2	3	5	…	102334155	12586269025

百度百科 - 斐波那契数列
斐波那契数列（Fibonacci sequence），又称黄金分割数列 [1]，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称“兔子数列”，其数值为：1、1、2、3、5、8、13、21、34……在数学上，这一数列以如下递推的方法定z义：F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。

※ 本题收获

递归算法的必备条件之一；
- 必然有出口，例如：if (n == 0) return; if (n > 0) n = n - 1;
计时方法
- C语言的时间计算方法；
- Java语言中的时间计算方法；
Java中有无static修饰对函数调用的影响。

代码（4种实现方法）

代码1（C语言经典递归 - 2种写法）


1
/* 
2
    1* 斐波那契数列的递归实现 
3
    2* 斐波那契数列第0项、第1项、第2项... 
4
    3* 主函数测试 
5

6
    测试样例1： n = 50, res = 12586269025
7
    测试样例2： n = 40, res = 102334155
8
*/ 
9

10
#include<stdio.h>
11

12
long long fibonacci(long long n)
13
{
14
    if (n == 0)
15
        return 0;
16
    if (n == 1)
17
        return 1; 
18
    if (n >= 2)
19
        return fibonacci(n-1) + fibonacci(n-2); 
20
 } 
21

22
/* 
23
    // line14~line19也可替换为如下两句：
24
    if(n==0 || n==1) return n;
25
    else return fibonacci(n-1) + fibonacci(n-2);
26
*/
27
 
28
 int main()
29
{
30
    // 先定义，后使用 
31
    long long n = 0;
32
    long long res = 0;
33
    
34
    scanf("%lld", &n); 
35
    res = fibonacci(n);               
36
    
37
    printf("%lld", res); //注意输出是 lld 
38
    return 0;
39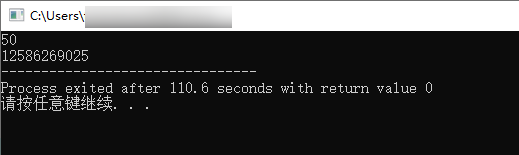
}

代码2（C语言经典递归 - 计时版）


xxxxxxxxxx
45
1
/* 
2
    1* 斐波那契数列的非递归实现 
3
    2* 斐波那契数列第0项、第1项、第2项... 
4
    3* 主函数测试 
5

6
    测试样例1： n = 50, res = 12586269025
7
    测试样例2： n = 40, res = 102334155
8
*/ 
9

10
#include<stdio.h>
11
#include<time.h>
12
// fibonacci 数列递归实现（long & 递归） 
13

14
long long fibonacci(long long n)
15
{
16
    if (n == 0)
17
        return 0;
18
    if (n == 1)
19
        return 1; 
20
    if (n >= 2)
21
        return fibonacci(n-1) + fibonacci(n-2); 
22
 } 
23

24
int main()
25
{
26
    // 先定义，后使用 
27
    clock_t start, end;
28
    double duration;
29
    
30
    long long n = 0;
31
    long long res = 0;
32
    
33
    scanf("%lld", &n); 
34
    
35
    start = clock();        //----包裹代码 
36
    res = fibonacci(n);               
37
    end = clock();          //----包裹代码
38
    
39
    duration = (double)(end - start) / CLOCKS_PER_SEC;  // 计算用时 
40
    
41
    printf("%lld\n", res); //注意输出是 lld 
42
    
43
    printf("%f seconds\n", duration);   // 输出用时 
44
    return 0;
45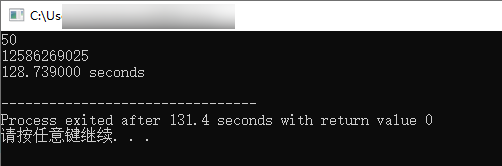
}

代码3（C语言非递归 - 计时版）


1
/* 
2
    1* 斐波那契数列的非递归实现 
3
    2* 斐波那契数列第0项、第1项、第2项... 
4
    3* 主函数测试 
5

6
    测试样例1： n = 50, res = 12586269025
7
    测试样例2： n = 40, res = 102334155
8
*/ 
9

10
#include<stdio.h>
11
#include<time.h>
12

13
// fibonacci 数列非递归实现（long & 非递归） 
14
long long fibonacci_nonRec(int n)
15
{
16
    long long f0 = 0;
17
    long long f1 = 1;
18
    long long fn = f1;  // fn表示 n>=2 
19
    while(n >= 2)
20
    {
21
        n = n - 1;
22
        fn = f1 + f0;   // 根据 f(n) = f(n - 1) + f(n - 2) 
23
        f0 = f1;        // f(n-2)先更新 
24
        f1 = fn;        // f(n-1)后更新 
25
    }
26
    return fn;
27
}
28

29
int main()
30
{
31
    // 先定义，后使用 
32
    clock_t start, end;
33
    double duration;
34
    
35
    long long n = 0;
36
    long long res = 0;
37
    
38
    scanf("%lld", &n); 
39
    
40
    start = clock();        //----包裹代码 
41
    res = fibonacci_nonRec(n);
42
    end = clock();          //----包裹代码
43
    
44
    duration = (double)(end - start) / CLOCKS_PER_SEC;  // 计算用时 
45
    
46
    printf("%lld\n", res); //注意输出是 lld 
47
    
48
    printf("%f seconds\n", duration);   // 输出用时 
49
    return 0;
50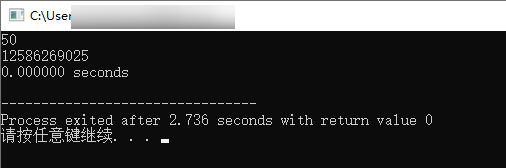
}

代码4（Java语言非递归 - 计时版）



1
// 这是一个类，名叫Fibcls
2

3
public class Fibcls {
4
    /**
5
     * 斐波那契数列： 
6
     * 测试样例1： n = 50, res = 12586269025 
7
     * 测试样例2： n = 40, res = 102334155
8
     */
9

10
    public static void main(String[] args) {
11
        // TODO Auto-generated method stub
12
        System.out.println("Hello, T!");
13

14
        long n = 50;
15

16
        // 时间单位选择[System.currentTimeMillis() || System.nanoTime()]
17
        long s1 = System.nanoTime();
18
        long nanoMul = 1000000000; // nanoTime 转为 seconds的倍数
19
        // 待计算时长的代码段放这里--------------┐
20

21
        System.out.println(fibonacci_R(n));
22

23
        // 待计算时长的代码段放这里--------------┘
24
        
25
        long e1 = System.nanoTime();
26
        float sec1 = (e1 - s1) / nanoMul;
27
        System.out.println("Elapsed Time(fibonacci_R): " + Float.toString(sec1) + " seconds.");
28

29
        
30
        
31
        long s2 = System.nanoTime();
32
        
33
        // 待计算时长的代码段放这里--------------┐
34
        // 解决方法2：实例化一个对象，然后调用非静态函数；
35
        
36
        // Step1. 用类实例化一个对象t
37
        Fibcls t = new Fibcls();
38
        
39
        // Step2. 调用非静态方法
40
        System.out.println(t.fibonacci_NonR(n));
41
        // 待计算时长的代码段放这里--------------┘
42

43
        long e2 = System.nanoTime();
44
        float sec2 = (e2 - s2) / nanoMul;
45
        System.out.println("Elapsed Time(fibonacci_NonR): " + Float.toString(sec2) + " seconds.");
46

47
    }
48

49
    // 递归解法
50
    public static long fibonacci_R(long n) {
51
        if (n < 0)
52
            return -1;
53
        if (n == 0)
54
            return 0;
55
        if (n == 1)
56
            return 1;
57

58
        return fibonacci_R(n - 1) + fibonacci_R(n - 2);
59
    }
60

61
    // 非递归解法
62
    public long fibonacci_NonR(long n) {
63
        long f0 = 0;
64
        long f1 = 1;
65
        long fn = f1;
66
        while (n >= 2) 
67
        {
68
            n = n - 1;
69
            fn = f1 + f0;
70
            // 注意f0和f1的更新顺序
71
            f0 = f1; // 先f0
72
            f1 = fn; // 再f1
73
        }
74
        return fn;
75
    }
76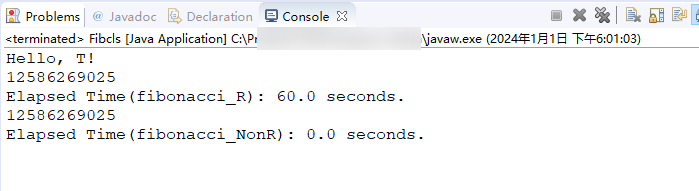
}

★ 知识点积累 (Java `static`方法的调用)


xxxxxxxxxx
1
// 这是一个类，名叫Fibcls
2

3
public class Fibcls {
4

5
    // main函数是有static修饰的方法
6
    public static void main(String[] args) {
7
        
8
        System.out.println(fibonacci_R(n));
9
        // 报错：Cannot make a static reference to the non-static method
10
        // fibonacci_R(long) from the type test
11
        // 翻译报错： 静态的main函数中，不能调用非静态函数
12
    }
13

14
    // 无static关键字
15
    public long fibonacci_R(long n) {...}
16

17
    // 无static关键字
18
    public long fibonacci_NonR(long n) {...}
19
}

问题 & 解决


xxxxxxxxxx
9
1
// 问题原因：
2
// 首先要理解以下几点：
3
// 1.static修饰的方法，无须产生类的实例对象就可以调用该方法，即static变量是存储在静态存储区的，不需要实例化。
4
// 2.非static修饰的方法，需要产生一个类的实例对象才可以调用该方法。
5
// 也就是说，在main函数中调用函数只能调用静态的。如果要调用非静态的，那么必须要先实例化对象，然后通过对象来调用非静态方法。
6

7
// 解决方法1：把非静态函数改为静态函数fibonacci_R
8
// Step1: [public long fibonacci_R(long n)] → [public static long fibonacci_R(long n)]
9
// Step2： 可以直接使用该方法了


x
1
// 这是一个类，名叫Fibcls
2

3
public class Fibcls {
4
    /**
5
     * 斐波那契数列： 
6
     * 测试样例1： n = 50, res = 12586269025 
7
     * 测试样例2： n = 40, res = 102334155
8
     */
9

10
    // main函数是有static修饰的方法
11
    public static void main(String[] args) {
12
        
13
        // main()函数里：调用有static关键字修饰的方法
14
        fibonacci_R(n);
15
        
16
        // main()函数里：调用无static关键字修饰的方法  
17
        // fibonacci_NonR(n); // 执行本行会报错
18
        
19
        // 解决方法：Step1 & Step2
20
        // Step1. 用类实例化一个对象
21
        Fibcls t = new Fibcls();
22
        // Step2. 调用非静态方法
23
        t.fibonacci_NonR(n);
24
    }
25

26
    // 有static关键字
27
    public static long fibonacci_R(long n) {...}
28

29
    // 无static关键字
30
    public long fibonacci_NonR(long n) {...}
31
}

[Coding017] 递归 - Fibonacci数列 递归知识点

知识点

※ 本题收获

代码（4种实现方法）

代码1（C语言经典递归 - 2种写法）

代码2（C语言经典递归 - 计时版）

代码3（C语言非递归 - 计时版）

代码4（Java语言非递归 - 计时版）

★ 知识点积累 (Java static方法的调用)

问题 & 解决

[Coding017] 递归 - Fibonacci数列
递归知识点

★ 知识点积累 (Java `static`方法的调用)